INTRODUCCIÓN
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común.
En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas.
Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas.
Una solución es todo par de números que cumple la ecuación.
En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Por ejemplo:
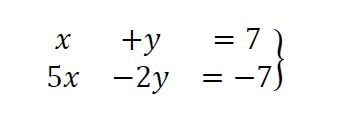
Sistema de ecuaciones: método de sustitución
A través del método de sustitución lo que debemos hacer es despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente. Lo veremos con más detalle en el siguiente ejemplo:
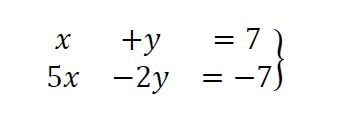
Lo primero que hacemos es despejamos una de las incógnitas en la primera ecuación.
x+y=7
x= 7-y
Posteriormente, sustituimos en la segunda ecuación el valor correspondiente de la «x».
5x-2y=-7
5.(7-y)-2y=-7
Ahora, despejamos la «y».
35-5y-2y=-7
35-7y=-7
-7y=-7-35
-7y=-42
y=-42/-7=6
y=6
Por último, utilizamos el valor de «y» para hallar el valor de «x».
x= 7-y
x=7-6=1
x=1
La solución de nuestro sistema es x=1 e y =6.
Sistema de ecuaciones: método de igualación
El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.
Los pasos a seguir son los siguientes:
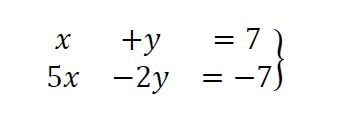
En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaré por la «x» y despejo la misma en ambas ecuaciones.
x+y=7; x=7-y
5x-2y=-7; 5x=2y-7; x=(2y-7)/5
Una vez hemos despejado, igualamos:
7-y=(2y-7)/5
5(7-y=(2y-7)/5)
35-5y=2y-7
42=7y
y=42/7=6
y=6
Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.
x=7-y
x=7-6=1
x=1
La solución de nuestro sistema es x=1 e y =6.
Sistema de ecuaciones: método de reducción
Con el método de reducción lo que hacemos es combinar, sumando o restando, nuestras ecuaciones para que desaparezca una de nuestras incógnitas.
Los pasos a seguir son los siguientes:
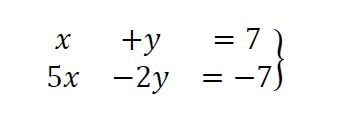
En primer lugar, necesitamos preparar las dos ecuaciones, si es necesario, multiplicándolas por los números que convenga.
En este caso, queremos reducir la «y» de nuestro sistema, por tanto, multiplicamos la primera ecuación por 2.
2(x+y=7)
5x-2y=-7
Así, el sistema se queda:

Si nos fijamos, sumando las ecuaciones la y nos desaparece.

Y nos quedaría:
7x=7
x=7/7=1
x=1
Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.
y= 7-x
y=7-1=6
y=6
La solución de nuestro sistema es x=1 e y =6.

Comentarios
Publicar un comentario